- Low Variance Craps Strategy For Dummies
- Low Variance Craps Strategy Examples
- Low Variance Craps Strategy Rules
- Low Variance Craps Strategy Definition

It is distribution variance that produces the familiar hot and cold streaks that we commonly experience at a craps table. The casino doesn’t care about the short-lived hot and cold streaks because the casino knows they occur only during short periods of time, and eventually the distribution approaches equilibrium and evens out. The probability of winning on a 4 or 10 in craps is (6/36)×(3/9) = 5.56%. Every time this happens you get an extra unit, so it is worth 5.56%. Normally the house edge on the come bet is 1.41%, so overall the player edge under this rule is 4.15%. So I agree that craps was the better game to play. Learn to Play Craps - Tips and Strategies - Variance. Retrieved August 15, 2020.
Low Variance Craps Strategy For Dummies
I’m writing a series of blog posts about casino games and the good and bad strategies for playing those games.
Craps is one of my favorite casino games, so I’ve been looking forward to writing this one.
And the beautiful thing about craps is that it’s a game of pure chance. The best strategy is just to choose the bets with the lowest edge for the house and have fun.
But I’ll have some things to say about some of the strategies and systems that other writers promote, too.
They’re mostly bad craps strategies.
Here’s the Only Craps Strategy You Need
When you’re dealing with an entirely random game – like craps – the only strategy that matters is choosing the bets with the lowest house edge and having fun.
I’ll have something to say about shooters and whether they have control over the outcomes later in this post, but for now, let’s just agree that games like craps are purely chance.
In other games that are entirely random, like slot machines, you don’t even really need to decide which bet to place. It’s chosen for you before you sit down.
When playing craps for real money, you have a handful of good bets you can make, but most of the bets on the table are bad. Just skip the bad bets, and you’re all set.
The Bests Bets at the Craps Table
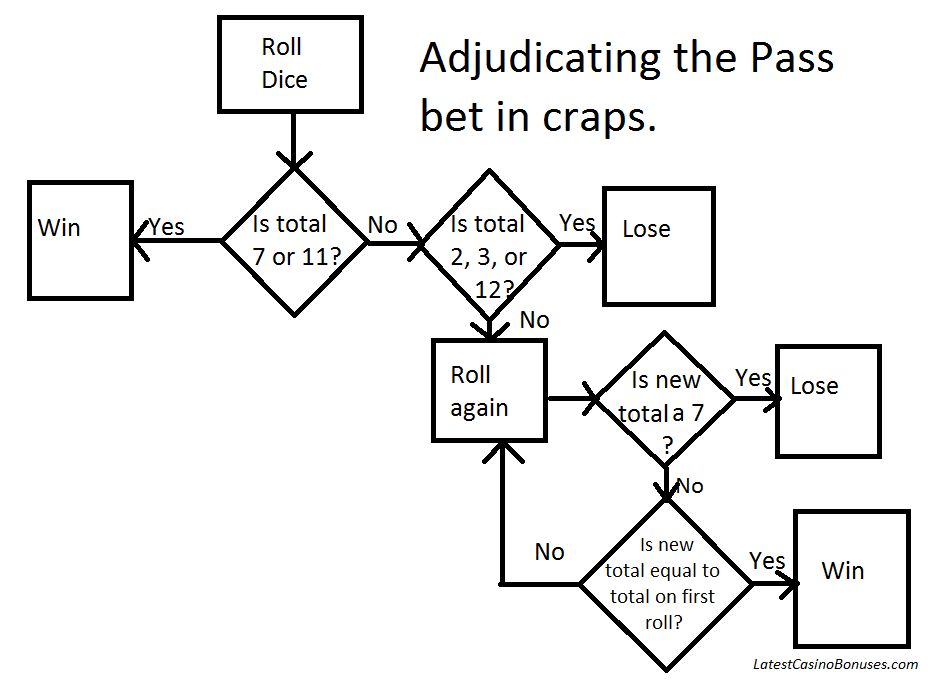
The best bets at the craps table are the pass line bet and the don’t pass bet.
The come and don’t come bets are also great wagers.
I always advise casino gamblers to try to limit their gambling to games where the house edge is lower than 2% — preferably 1.5% or lower.
The house edge for the pass and come bets is the same, 1.41%, which means they qualify.
The house edge for the don’t pass and don’t come bets is even lower, 1.36%, but the 0.05% isn’t worth worrying about. Most people prefer to root for the shooter to succeed.
The other bet to think about at the craps table is the odds bet. This is a bet you can only place after making one of the 4 bets I already mentioned and when the shooter has set a point.
This is one of the only bets in the casino that has no house edge. It’s a break-even bet, but it can be expensive.
It can also drive the effective house edge on the money you have in action down to almost nothing.
Here’s how that works.
How the Odds Bet Changes the House Edge for the Better
If you’re betting on the pass line and the shooter sets a point, you can expect to lose $1.41 for every $100 you bet. That’s on average and in the long run.
If you’re playing at a casino that only allows you to place an odds bet at 1X the size of your pass line bet, you can put another $100 into action.
Your expected loss remains $1.41, though, which effectively cuts the house edge in half, from 1.41% to 0.71%.
If you’re able to bet 2X your original bet on the odds bet, you can lower that even further to 0.36%. (You have $300 in action, but your expected loss is still only $1.41.)
The more you’re able to bet on the odds bet, the lower the house edge for all the money you have in action becomes.
It’s clear why betting on the pass line and taking the most odds that you can is an effective strategy. With the odds bet, you can get the house edge in craps lower than 0.5% at least some of the time at the table, making it an even better game than blackjack.
And what’s more, you don’t have to memorize basic strategy to get the low house edge at craps.
You just need a big enough casino bankroll to make the right bets, and you need enough sense to avoid the bad bets at the table – of which there are many.
Any Strategy that Involves Placing ANY Other Bets at the Craps Table Is a BAD Craps Strategy
There’s a reason gambling experts measure bets according to their house edge. That’s because it’s the single best indicator of how good or bad a bet is.
The house edge is a statistical estimate of how much money you’ll lose as a percentage of your original bet over the long run.
If the house edge is 1.41%, the casino expects to win an average of $1.41 every time you bet $100.
If the house edge is 16.66%, the casino expects to win an average of $16.66 every time you bet $100.
Which bet looks like the better bet for the casino?
And which one looks like the better bet for the gambler?
It shouldn’t be hard to make the distinction.
Even the best of the bad bets on the craps table are inferior to the 1.41% or 1.36% you can get from the pass, don’t pass, come, and don’t come bets.
And trust me on this:
You can have PLENTY of fun sticking with the basic bets at the craps table.
Betting Systems Where You Raise and Lower the Size of Your Bets Are Bad Strategies
The classic example of this kind of betting system is the Martingale System, where you double the size of your bets after each loss. When you do this repeatedly, you eventually win back the money you’ve lost along with a profit of one unit.
The problem with a system like the Martingale is that you’ll eventually run into a big enough losing streak that it will wipe out all those small profits and then some.
Most people underestimate how quickly a bet’s size gets when doubling after every loss.
They also overestimate how likely they are to avoid long losing streaks.
If you double a $5 bet once, that’s $10.
But if you run into a losing streak of 8 bets in a row, you’re looking at having to bet $640 to make up for your losses.
Also, every roll of the dice is an independent event. The odds don’t change based on how many times you’ve won or lost in a row.
You might think the probability of losing that 8th bet is lower than the likelihood of losing the first one, but the truth is that the dice have no memory. They have the same 6 sides, no matter how many times you’ve lost in a row.
Each bet in craps is an independent event, and any betting system will assume that the odds are changing based on how many times in a row you’ve won or lost.
Money Management Strategies Don’t Hurt Anything, but They Won’t Improve Your Odds of Winning, Either
Money management strategies involve having strict gambling discipline about how much of your bankroll you’re willing to risk before quitting the game. They also require you to stop when you’ve won an arbitrary amount of money.
Money management techniques are often used in conjunction with betting systems.
Here’s an example of a money management strategy in craps:
Low Variance Craps Strategy Examples
You decide your bankroll for the session is $250, and you’re playing for $5 per roll of the dice.
Your stop-loss limit is $100, so, if your bankroll drops to $150, you must quit the craps session and go do something else.

Your win goal is $250, so once your bankroll gets up to $500, you must quit the game and go do something else.
This kind of strategy might increase your chances of walking away from the game a winner.
But that’s only because a lot of gamblers will just keep playing until they’ve lost their entire stake. They just don’t generally have a lot of sense about that sort of thing.
The Jury’s Out on Dice Setting or Dice Control
I’ve seen multiple reputable gambling writers express interest and some belief that some craps shooters can influence the probability of specific outcomes. I’m skeptical – in the extreme – but I’ll give it an appropriate amount of credence.
The idea is that you hold the dice a specific way – “setting” the dice – then throw with a minimum amount of force – just enough to hit the back wall and eliminate most of the rolling action.
A controlled shooting expert doesn’t have to be perfect. Instead, they’re trying to be like someone who’s playing darts. They improve the probability enough to change the negative expectation on a bet to a positive expectation.
You can buy books and videos explaining how to get an edge at craps this way, but I can’t imagine the amount of practice and record-keeping required to have any confidence in your ability to change the odds.
Imagine if you spent 1000 hours trying to learn how to control the dice and coming up short. Maybe you just don’t have the knack for it.
That doesn’t sound like a good deal to me.
I’d rather learn to count cards in blackjack.
Conclusion
Those are the best and the worst of the strategies I know of for playing craps in the casino. I know plenty of people who would disagree with every recommendation I’ve made, but the math behind the game doesn’t lie.
The best strategy is to stick with the bets with the lowest house edge and have as much fun as you can.
Learn to Play Craps – Here are some tips and strategies and a guide to Variance in Craps
If the casino has such an advantage over the player, why on Earth does anyone play the game? My guess is that most people don’t have a clue they’re playing a losing game. Others are so arrogant they think they can outplay the casino and turn a negative expectation into a positive, even over the long term.
Others know they’ll lose, but play anyway for fun and excitement. As a knowledgeable player, why should you even bother playing a game you know will beat you? As a knowledgeable player, is there any hope you can walk away a winner, at least once in a while, even though you’re at a statistical disadvantage?
You can’t win a predetermined game
Craps is a game of numbers and statistics, with the house having a built-in advantage. Since craps is based on statistics, let’s find a way to use statistics to our advantage. You’ll never beat the casino over the long haul, but you can, indeed, beat it in the moments of time when the distribution hiccups and things go your way.
Let’s talk about “variance,” which is the average squared deviation of each number from the mean of a data set. Huh? Don’t worry; we don’t need a Harvard math degree to understand this. It’s simply a measure of how spread out the data is. Let’s consider the familiar coin-flip example.
Suppose we flip a coin 10,000 times. We expect heads to appear about 5,000 times and tails to appear about 5,000 times. Suppose we bet $1 on heads for each flip. If these are even-money bets, we expect to break even–or close to it after those 10,000 flips. As illustrated in one of my other articles, the house doesn’t give us even money when it loses. In our coin-flip example, instead of paying us $1 for each loss, suppose they pay us only $0.96. With this built-in house advantage, our negative expectation is to lose about $200 after 10,000 flips. Here’s the math. If we expect about 5,000 heads and about 5,000 tails to appear, then we expect to lose 5000 x $1 = $5000; and win 5000 x $0.96 = $4800. $5000 – $4800 = $200. This is called “negative expectation.”
Now, of those 10,000 flips, suppose we focus on only 30 of them, and we continue betting on heads. Of those 30 flips, we might see heads 25 times and tails only 5 times. This data fluctuation shows that, for a limited number of flips over a short period of time, we can get lucky and experience Nirvana where things go our way. I call it a “Nirvana hiccup” in the distribution that causes a relatively high variance. In this example of only 30 flips, we win $24 for the 25 heads (i.e., 25 x $0.96 = $24), and lose $5 for the 5 tails (i.e., 5 x $1 = $5), which gives us a net win of $19. This short term variance temporarily removes the long-term negative expectation, which means there are, indeed, times when we can walk away a winner.
Variance, the reasons casinos and craps flourishes
Low Variance Craps Strategy Rules
Although you’ll lose in the long-term, there are times when you’ll win because of variance. Suppose you take a three day vacation in Vegas once a year and play four one hour craps sessions each day (i.e., a total of 12 hours for the trip). You could conceivably get extremely lucky and hit that Nirvana hiccup during each session, and then go home a big winner. In that case, you go home thinking you’re a genius, a craps god, invincible, a world-class gambling stud. Yeah, sure, okay. I don’t recommend quitting your day job.
Now, suppose you’re a Vegas local who plays an hour every day after work. In this case, it’s clear that whatever few Nirvana hiccups you experience will be properly adjusted over time such that you’ll lose your shirt in the long-term.
Therefore, the infrequent craps player can, indeed, consistently win if she’s lucky enough to hit those Nirvana hiccups. However, the frequent long term player has no chance of coming out a winner at the end of his craps life. Part of the secret to craps is knowing how to be around for those occasional Nirvana hiccups where the dice fall your way.
If you don’t want to lose your shirt, you must learn the secret to craps. Don’t fall for bogus winning systems or ridiculous dice-setting claims. Distribution variance is the only thing that makes you a short-term winner. Nothing else. No silly dice setting technique. No bogus winning system. It’s the distribution variance and nothing else. Got it? Be smart. Play smart. Learn the secret to craps.
Low Variance Craps Strategy Definition
Now you know!